Comment est calculée la rémunération de votre épargne ?

Fiche économique E 04

Date de publication : 28/11/2018 - Banque/argent

Vous avez pour projet de placer une partie de votre revenu sur un livret ou un autre placement rémunérateur et vous souhaitez savoir combien cela va vous rapporter ?

Si vous souhaitez connaître votre rémunération suite à un placement, cette fiche a pour objet de présenter quelques notions de mathématiques financières afin de mieux comprendre les mécanismes de la rémunération de l’épargne dans trois cas différents : le taux d’intérêt simple, les taux d’intérêt composés, et les intérêts perçus lors de versements périodiques.

Attention, cette fiche ne présente pas les mécanismes de fixation des différents taux appliqués sur les différents produits existants (livrets, plan d'épargne ...).

1 - Le taux d'intérêt : la rémunération de l'épargne

2 - Le taux d'intérêt simple

3 - Les taux d'intérêt composés

4 - Les intérêts lors de versements périodiques

1 - Le taux d’intérêt : la rémunération de l’épargne

Le taux d’intérêt représente la rémunération d’une personne physique ou morale quand celle-ci prête une somme d’argent (qu’on appelle le capital). La rémunération est payée par la personne physique (vous par exemple) ou morale (une banque, une entreprise, une association …) à qui le capital est prêté.

Par exemple, si la banque vous octroie un crédit immobilier, c’est la banque qui vous prête un capital. La rémunération de celle-ci est alors la différence entre ce qu’elle vous prête et ce que vous lui remboursez au final. Cette différence est déterminée par le taux d’intérêt.

A l’inverse, si vous placez de l’argent sur un livret par exemple, c’est comme si vous prêtiez un capital à la banque. Et vous êtes rémunérés pour ce prêt. Par exemple, imaginons que vous placez 100 € pendant un an sur un livret rémunéré à 10 %. A la fin de l’année, vous récupérez 110 €. Ce qui représente la somme entre votre capital initial (100 €) et les intérêts perçus sur l’année (10 % de 100 €, soit 10 €). La rémunération du prêteur est donc de 10 €.

2 - Le taux d’intérêt simple

Le taux d’intérêt simple permet de calculer la rémunération d’un placement sur le court terme (pour une durée inférieure ou égale à un an).

La formulé générale de calcul des intérêts perçus sur la période est la suivante :

Avec I : intérêts perçus sur la période

C : capital initialement investi

i : taux d’intérêt exprimé en pourcentage

n : période du placement.

Les taux d’intérêt sont dans la plupart des cas exprimés sur un an. Ainsi, le calcul des intérêts perçus se fera au prorata de la période écoulée si elle est inférieure à un an. Par exemple, si la durée du placement est de 9 mois, alors n = 9/12 ; pour une période de 187 jours, n=187/365.

Dans les cas d’une durée journalière, le nombre de jours dans l’année peut différer entre 360 jours (on appelle cela « l’année lombarde » qui est parfois utilisée pour simplifier les calculs, car c’est un nombre plus facilement divisible, et chaque mois est de la même durée, de 30 jours), 365 jours ou 366 jours. Pensez à vous renseigner avant.

1^er exemple : J’ai placé 2 500 € pendant un an à un taux d’intérêt annuel de 3 %. Combien cela va-t-il me rapporter ?

En appliquant la formule, on obtient :

Ainsi, au bout d’un an, les intérêts perçus sont de 75 €. La valeur finale du placement correspond au capital initialement investi (2 500 €) auquel s’ajoute les intérêts perçus (75 €), soit 2 575 €.

2^ème exemple : J’ai placé 4 000 € pendant 142 jours à un taux d’intérêt annuel de 2,5 %. Combien cela va-t-il me rapporter ?

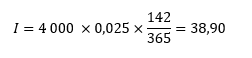
Les intérêts perçus sont de 38,90 €, la valeur finale du placement est de 4 038,90 €.

3^ème exemple : Je souhaite que la valeur finale de mon placement au bout de trois ans soit de 8 000 €. Sachant que le taux annuel est de 2 %, combien dois-je place initialement ?

Ici, on cherche à connaître C, le placement initial sachant que les taux d’intérêts perçus ajoutés à la valeur initiale du placement doivent être égaux à 8 000 €. Autrement dit : I + C = 8000.

On note V, la valeur finale du placement, qui est donc égale à : V = I + C

En modifiant la formule de base, on obtient :

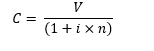
Pour notre exemple, on a alors :

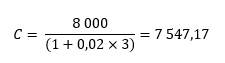
Ainsi, pour obtenir 8 000 € au bout de trois ans à un taux annuel de 2 %, il faut placer initialement 7 547,17 €.

3 - Les taux d’intérêt composés

Les taux d’intérêt composés permettent de calculer la rémunération d’un placement sur le long terme (pour une durée supérieure à un an). En effet, les taux d’intérêt composés permettent d’intégrer les intérêts perçus de la première année au capital initial, qui porteront eux-mêmes des intérêts.

Par exemple, si on place 1 500 € pendant deux ans à un taux annuel de 3 %. A la fin de la première année, les intérêts perçus seront de 1 500 x 0,03, soit 45 €. Le capital acquis au bout d’un an sera de 1 545 €. Et c’est ce capital qui sera rémunéré pour la seconde année (1 545 x 0,03 = 46,35). Chaque année les intérêts perçus vont augmenter car le capital sera valorisé des intérêts acquis des périodes précédentes.

Pour une période courte, le calcul est assez simple et rapide. Mais si vous souhaitez connaître la rémunération de votre placement sur 10 ou 20 ans, cela devient plus complexe. Il faut donc appliquer la formule suivante pour calculer la valeur capitalisée quand il s’agit d’un placement de longue période :

Avec C_n : valeur capitalisée (capital initial + intérêts acquis au cours de la période) au bout de n années

C : capital initial

i : taux d’intérêt annuel en pourcentage

n : nombre d’années

1^er exemple : Je place 20 000 € pendant 10 ans à un taux annuel de 4 %. Combien cela me rapporte-t-il ?

Au bout des dix ans, la valeur capitalisée sera de 29 604,89 €. Les intérêts perçus sur la période sont de 9 604,89 € (29 604,89 – 20 000).

2^ème exemple : Je souhaite obtenir 150 000 € dans 7 ans sur un placement à un taux annuel de 3,5 %. Combien dois-je placer aujourd’hui ?

Ici, c’est la valeur du capital initial (C) que nous cherchons, et nous connaissons la valeur capitalisée (C_n = 150 000). En faisant varier la formule on obtient :

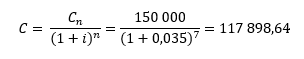
Il faut placer initialement 117 898,64 € pendant 7 ans, pour obtenir 150 000 €.

4 - Les intérêts lors de versements périodiques

Ici, nous sommes dans le cas où on effectue des versements réguliers sur un compte rémunéré. On cherche à connaître la valeur finale acquise par ces versements réguliers. La formule générale est alors la suivante :

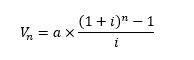
Avec Vn : valeur acquise

a : montant du versement

i : taux d’intérêt annuel exprimé en pourcentage

n : durée.

On suppose ici sur les versements sont égaux.
Cette formule suppose que le dernier versement a été versé, mais non rémunéré.

1^er exemple : Je place 1 200 € par an pendant 9 ans à un taux annuel de 2,5 %. Quelle sera l’épargne au terme ?

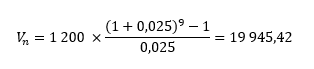
Au bout des neuf ans, l’épargne sera de 19 945,42 €.

2^ème exemple : Combien dois-je placer par an à un taux annuel de 5 % pour obtenir 150 000 dans 10 ans ?

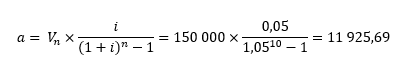
Pour obtenir 150 000 € au bout de 10 ans à un taux annuel de 5 %, il faut placer 11 925,69 € par an.

Il ne faut pas confondre un taux proportionnel ou actuariel :

Un taux proportionnel est un taux qui unit le taux d’intérêt à sa période. Ainsi, un taux annuel de 12 % correspond à un taux mensuel de 1 %, ou à un taux trimestriel de 3%.
Un taux d’intérêt actuariel prend en compte la technique des intérêts composés. Sa formule générale est la suivante :